Prostokrąg (2) - Wpisany w prostokąt

Data ostatniej modyfikacji:
2018-09-15

Autor:

Krzysztof Omiljanowski

pracownik IM UWr

Dział matematyki:

geometria syntetyczna

Poziom edukacyjny:

gimnazjum

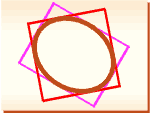
Obiektem naszych badań będzie owal z rysunku, nazywany prostokręgiem, którym zajmowaliśmy się już wcześniej tutaj - przeczytaj koniecznie!
Widać, że można opisać na nim wiele prostokątów.
Jak je konstruować? Jakie mają własności? Poszukajmy wspólnie odpowiedzi na te pytania.

Przypomnijmy: owal na rysunku jest prostokręgiem zbudowanym z czterech ćwiartek dwóch okręgów dwie mniejsze ćwiartki mają promień r₁, a dwie większe mają promień r₂ (patrz rysunki poniżej).

Jest wiele prostokątów opisanych na danym prostokręgu. Poprzednio zbadaliśmy tylko taki przypadek, gdy boki prostokąta były równoległe do średnic prostokręgu. Obejrzyjmy teraz wszystkie prostokąty opisane na dwóch prostokręgach. Eksperymentuj na poniższych modelach.

przytrzymaj:

przytrzymaj:

Widać (a może tylko wydaje się), że zachodzi:

TWIERDZENIE 1. Na prostokręgu można opisać kwadrat.

TWIERDZENIE 2. Dla prostokręgu, który nie jest okręgiem, kwadrat opisany na nim jest tylko jeden i jego boki ze średnicami prostokręgu. Inaczej mówiąc: jego przekątne są

TWIERDZENIE 3. Pole kwadratu opisanego na prostokręgu jest równe [tex] (r_1+r_2)^2 [/tex].

Jedynie trzecie twierdzenie warte jest chwili zastanowienia. Jak je pokazać?

Wskazówka do dowodu tw. 3.

Jednak najciekawsze wydaje się takie zadanie.

ZADANIE 1. Mając dany prostokrąg i punkt A na jego brzegu, skonstruować prostokąt opisany na tym prostokręgu zawierający punkt A na brzegu.

Wskazówka 1. do zad. 1.

Wskazówka 2. do zad. 1.

Wskazówka 3. do zad. 1.

Rozwiązanie zad. 1.

Skoro wiemy już, jak konstruować prostokąty opisane na prostokręgu, można zadać rutynowe pytania.

ZADANIE 2. Który z prostokątów opisanych na danym prostokręgu
ma ^największe/_najmniejsze pole?

ZADANIE 3. Który z prostokątów opisanych na danym prostokręgu
ma ^największy/_najmniejszy obwód?

Oczywiście o 'ekstremalne zachowanie' można podejrzewać 'skrajne' prostokąty, które już częściowo były badane: kwadrat oraz prostokąt o bokach równoległych do średnic prostokręgu.

Pewnym zaskoczeniem może być

Odpowiedź do zad. 3.