Zad. 1. Znajdź najmniejszą liczbę całkowitą dodatnią taką, że 3% tej liczby oraz 7% tej liczby są liczbami całkowitymi i mają w rzędzie jedności tę samą cyfrę.
Zad. 2. W układzie współrzędnych dany jest kwadrat o wierzchołkach A = (4, 4), B = (4, -4), C = (-4, -4), D = (-4, 4). W wierzchołku A siedzi mrówka, a w wierzchołku C - biedronka. W pewnym momencie obie rozpoczynają wędrówkę po brzegu kwadratu w kierunku zgodnym z kierunkiem ruchu wskazówek zegara. Mrówka idzie z prędkością 13 jednostek na minutę, a biedronka - 9 jednostek na minutę. Po jakim czasie nastąpi ich pierwsze spotkanie? W jakim punkcie ono nastąpi?
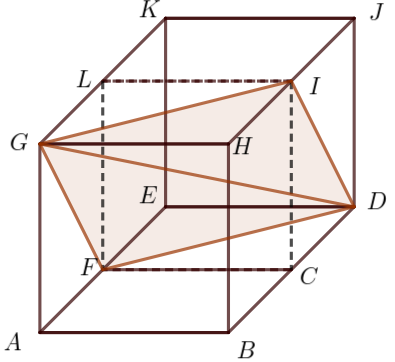
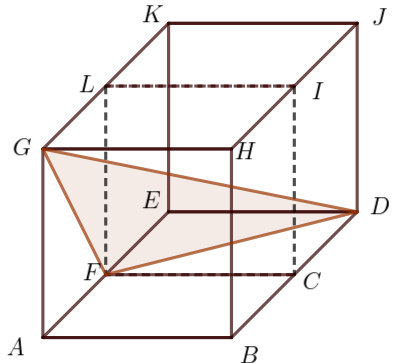
Zad. 3. Dwa jednakowe sześciany ABCFGHIL oraz FCDELIJK umieszczono jeden obok drugiego jak na rysunku. Oblicz miary kątów trójkąta GFD.
W kwietniu punkty zdobyli:
- 3 – Darya Karnitskaya SP 107 Wrocław, Yaraslau Sialiuk SP 82 Wrocław, Wiktor Szwarczyński SP Szkoła w Chmurze Poznań, Jan Węgrzyn SP 44 Wrocław, Ignacy Włodarski SP 36 Wrocław;
- 2,5 – Filip Staszkiewicz SP 50 Wrocław, Michał Wróblewski SP Bielkówko;
- 2 – Jakub Derewecki SP 50 Wrocław, Antoni Gałkowski SP Józefów n. Wisłą, Stanisław Góralski SP Józefów n. Wisłą, Claudia Jończyk SP Jedlnia Letnisko, Paweł Jarzyński SP 13 Zielona Góra, Adam Kosarzycki SP 16 Wrocław, Amelia Łakomiec SP 50 Wrocław, Hanna Łukasik SP 50 Wrocław, Alicja Picińska SP 64 Wrocław, Stanisław Solski SP 13 Zielona Góra, Dawid Zysk SP 19 Legnica;
- 1 – Szczepan Buczkowski SP 2 Ożarów Mazowiecki, Anita Głowacz SP Popielów, Wiktor Nobis SP Iłża, Natalia Pisz SP Dobrzeń Wielki, Tymoteusz Pysz SP ŻAR Gliwice.
Pozostali uczestnicy otrzymali poniżej 1 punktu.
Zad. 1. Niech x oznacza szukaną liczbę. Ponieważ 3% liczby x to 0,03x, a wynik ma być całkowity dodatni, więc x musi być podzielne przez 100. Zatem x=100k, gdzie k ϵ {1, 2, 3, …}. Wówczas 3% liczby x to 0,03·100k=3k, a 7% liczby x to 0,07⋅100k=7k. Dla k=5 liczby 3k i 7k mają tę samą cyfrę jedności. Liczba x jest zatem równa 100⋅5=500.
Zad. 2. Odległość między mrówką a biedronką jest równa połowie obwodu kwadratu, czyli 16 jednostkom. W czasie minuty mrówka przybliża się do biedronki o 13–9=4 jednostki. Do pierwszego spotkania dojdzie po 16:4=4 minutach. Biedronka przejdzie w ciągu 4 minut 4·9=36 jednostek, czyli zrobi jedno pełne okrążenie i przejdzie jeszcze 4 jednostki. Pierwsze spotkanie nastąpi więc w punkcie (-4, 0).
Zad. 3. Zauważmy, że punkt I leży na płaszczyźnie zawierającej trójkąt GFD. Odcinki GF, FD, DI, IG i FI są równej długości, czyli czworokąt GFDI jest rombem o kącie ostrym 60° (bo trójkąt GFI jest równoboczny). Zatem |∢GFD|=120°, |∢FGD|=|∢FDG|=30°.
To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
